No nosso último papo, desmistificamos a Inteligência Artificial e vimos como Python é o parceiro ideal para quem quer começar nessa jornada. Agora, chegou a hora de colocar a mão na massa e construir nosso primeiro algoritmo de IA de verdade! E vamos começar com um dos algoritmos mais fundamentais e didáticos: a Regressão Linear.
Se o nome parece complicado, relaxa! 😉 Em outras palavras, Regressão Linear é uma técnica simples e poderosa para entender e prever relações entre diferentes informações. Neste post, vamos explorar o conceito por trás da Regressão Linear, entender como ela funciona e, principalmente, construir um modelo funcional em Python passo a passo. Prepare-se para dar vida à IA na prática! 🚀
Regressão Linear: Desvendando a relação entre os dados 🤓
Primeiramente, vamos entender o que a Regressão Linear realmente faz. Imagine que você quer prever o preço de uma casa com base no seu tamanho. Intuitivamente, sabemos que casas maiores tendem a ser mais caras, certo? A Regressão Linear entra em cena para formalizar essa intuição!
Em essência, a Regressão Linear busca encontrar uma relação linear entre uma variável que queremos prever (chamada de variável dependente ou alvo) e uma ou mais variáveis que usamos para fazer essa previsão (chamadas de variáveis independentes ou características). No nosso exemplo da casa, o preço seria a variável dependente, e o tamanho da casa, a variável independente.
Graficamente, podemos pensar na Regressão Linear como encontrar a melhor linha reta que representa a relação entre essas variáveis em um gráfico de dispersão. Essa linha reta é o nosso modelo de Regressão Linear! Uma vez que temos essa linha, podemos usá-la para prever o valor da variável dependente para novos valores das variáveis independentes.
Por exemplo, se encontrarmos a linha de Regressão Linear que relaciona tamanho da casa e preço, podemos usar essa linha para prever o preço de uma casa de um tamanho que nunca vimos antes! É como ter uma “fórmula mágica” para fazer previsões! ✨
Mão na massa: Regressão linear em Python com Scikit-Learn 💻
Agora que entendemos o conceito, vamos para a parte mais divertida: o código! Vamos usar a biblioteca scikit-learn, que é simplesmente fantástica para Machine Learning em Python. Ela já tem tudo o que precisamos para implementar Regressão Linear de forma rápida e fácil.
Instalação das bibliotecas necessárias
Primeiro passo, instale as bibliotecas necessárias usando o pip:
pip install numpy matplotlib scikit-learn
Importação das dependências
Em seguida, crie um arquivo python em seu editor preferido e vamos importar as bibliotecas que vamos usar:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score- numpy (np): Biblioteca essencial para computação numérica em Python. Usaremos para criar e manipular arrays de dados.
- matplotlib.pyplot (plt): Biblioteca para criar gráficos e visualizações. Usaremos para visualizar nossos dados e o modelo de Regressão Linear.
- sklearn.linear_model.LinearRegression: Classe do scikit-learn que implementa o algoritmo de Regressão Linear.
- sklearn.metrics.mean_squared_error e sklearn.metrics.r2_score: Funções para avaliar o desempenho do nosso modelo.
Criando o conjunto de dados de treino
Em seguida, vamos criar um conjunto de dados simples para o nosso exemplo. Imagine que estamos medindo o tempo de estudo de alguns alunos e suas notas em uma prova. Queremos ver se existe uma relação entre tempo de estudo e nota.
# Dados de exemplo: Tempo de estudo (horas) e Nota na prova
tempo_estudo = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # Reshape para formatar como matriz coluna
notas = np.array([2, 4, 5, 4, 6, 8, 7, 9, 8, 10])- tempo_estudo: Nosso array com o tempo de estudo em horas. Usamos
.reshape(-1, 1)para garantir que ele tenha o formato de uma matriz coluna, que é o formato esperado pelo scikit-learn para variáveis independentes. - notas: Nosso array com as notas correspondentes.
Criando o modelo de Regressão Linear
Agora, vamos criar e treinar nosso modelo de Regressão Linear!
# Criar o modelo de Regressão Linear
modelo = LinearRegression()
# Treinar o modelo com os dados
modelo.fit(tempo_estudo, notas)- modelo = LinearRegression(): Criamos uma instância da classe LinearRegression. Este é o nosso modelo de Regressão Linear “virgem”, ainda sem aprender nada.
- modelo.fit(tempo_estudo, notas): Aqui acontece a mágica! Usamos o método
.fit()para treinar o modelo. Nesse passo, o algoritmo de Regressão Linear analisa os dados de tempo_estudo e notas e encontra a melhor linha reta que se ajusta a esses dados. É nesse momento que o modelo “aprende” a relação entre as variáveis.
Fazendo previsões com o modelo treinado
Com o modelo treinado, podemos fazer previsões! Vamos prever a nota de um aluno que estudou 5.5 horas:
# Fazer previsões
tempo_estudo_predicao = np.array([5.5]).reshape(-1, 1) # Tempo de estudo para prever
nota_predita = modelo.predict(tempo_estudo_predicao)
print(f"Nota predita para 5.5 horas de estudo: {nota_predita[0]:.2f}")- tempo_estudo_predicao: Criamos um array com o tempo de estudo para o qual queremos fazer a previsão. Novamente, usamos
.reshape(-1, 1)para formatar corretamente. - nota_predita = modelo.predict(tempo_estudo_predicao): Usamos o método
.predict()do modelo treinado para fazer a previsão. O modelo usa a linha de Regressão Linear que aprendeu para estimar a nota correspondente a 5.5 horas de estudo. - print(…): Imprimimos a nota predita, formatando para duas casas decimais.
Exibindo o modelo graficamente
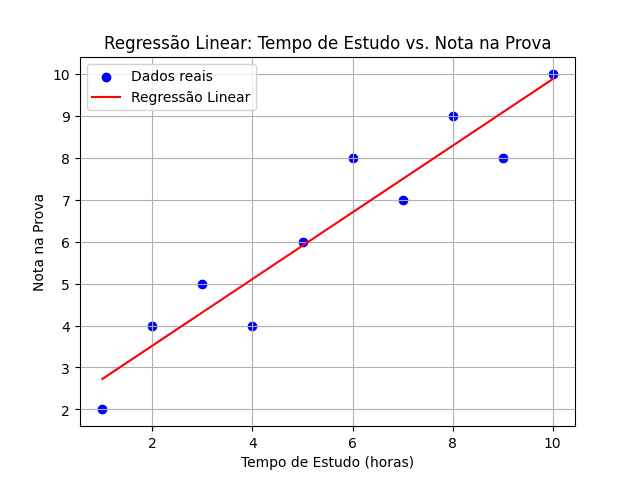
Para visualizar o resultado, vamos plotar os dados e a linha de Regressão Linear:
# Visualizar os resultados
plt.scatter(tempo_estudo, notas, color='blue', label='Dados reais') # Plotar os dados reais
plt.plot(tempo_estudo, modelo.predict(tempo_estudo), color='red', label='Regressão Linear') # Plotar a linha de regressão
plt.xlabel('Tempo de Estudo (horas)')
plt.ylabel('Nota na Prova')
plt.title('Regressão Linear: Tempo de Estudo vs. Nota na Prova')
plt.legend()
plt.grid(True)
plt.show()- plt.scatter(…): Cria um gráfico de dispersão dos dados reais (tempo de estudo vs. notas).
- plt.plot(…): Plota a linha de Regressão Linear. Usamos modelo.predict(tempo_estudo) para obter as notas preditas para os tempos de estudo originais e plotar a linha.
- plt.xlabel(…), plt.ylabel(…), plt.title(…): Define os rótulos dos eixos e o título do gráfico.
- plt.legend(): Exibe a legenda para identificar os dados reais e a linha de regressão.
- plt.grid(True): Adiciona uma grade ao gráfico para facilitar a leitura.
- plt.show(): Exibe o gráfico.
Avaliação do modelo
Finalmente, para avaliar o quão bom é o nosso modelo, podemos usar algumas métricas. Vamos calcular o Erro Quadrático Médio (Mean Squared Error – MSE) e o Coeficiente de Determinação (R-squared):
# Avaliar o modelo
notas_preditas_treino = modelo.predict(tempo_estudo) # Previsões nos dados de treino
mse = mean_squared_error(notas, notas_preditas_treino)
r2 = r2_score(notas, notas_preditas_treino)
print(f"Erro Quadrático Médio (MSE): {mse:.2f}")
print(f"Coeficiente de Determinação (R²): {r2:.2f}")- notas_preditas_treino = modelo.predict(tempo_estudo): Fazemos previsões usando o modelo nos próprios dados de treino para poder comparar com as notas reais.
- mse = mean_squared_error(…): Calcula o Erro Quadrático Médio, que mede a média dos erros ao quadrado entre as notas reais e as notas preditas. Quanto menor o MSE, melhor o modelo.
- r2 = r2_score(…): Calcula o Coeficiente de Determinação (R²), que varia de 0 a 1 e representa a proporção da variância nas notas que é explicada pelo modelo. Quanto mais próximo de 1, melhor o modelo se ajusta aos dados.
- print(…): Imprimimos os valores de MSE e R².
Código completo:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Dados de exemplo: Tempo de estudo (horas) e Nota na prova
tempo_estudo = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
notas = np.array([2, 4, 5, 4, 6, 8, 7, 9, 8, 10])
# Criar o modelo de Regressão Linear
modelo = LinearRegression()
# Treinar o modelo com os dados
modelo.fit(tempo_estudo, notas)
# Fazer previsões
tempo_estudo_predicao = np.array([5.5]).reshape(-1, 1)
nota_predita = modelo.predict(tempo_estudo_predicao)
print(f"Nota predita para 5.5 horas de estudo: {nota_predita[0]:.2f}")
# Visualizar os resultados
plt.scatter(tempo_estudo, notas, color='blue', label='Dados reais')
plt.plot(tempo_estudo, modelo.predict(tempo_estudo), color='red', label='Regressão Linear')
plt.xlabel('Tempo de Estudo (horas)')
plt.ylabel('Nota na Prova')
plt.title('Regressão Linear: Tempo de Estudo vs. Nota na Prova')
plt.legend()
plt.grid(True)
plt.show()
# Avaliar o modelo
notas_preditas_treino = modelo.predict(tempo_estudo)
mse = mean_squared_error(notas, notas_preditas_treino)
r2 = r2_score(notas, notas_preditas_treino)
print(f"Erro Quadrático Médio (MSE): {mse:.2f}")
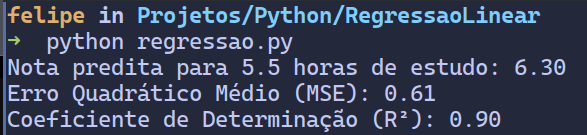
print(f"Coeficiente de Determinação (R²): {r2:.2f}")Executando este código, você verá um gráfico com os pontos de dados e a linha de Regressão Linear, além disso, verá a nota predita para 5.5 horas de estudo e as métricas de avaliação do modelo.
Parabéns! Você Construiu Seu Primeiro Algoritmo de IA! 🎉
Por fim, com este post, você não só aprendeu o conceito de Regressão Linear, mas também colocou a mão na massa e construiu um modelo funcional em Python! Isso é Inteligência Artificial na prática!
Lembre-se, este é apenas o começo! A Regressão Linear é um algoritmo fundamental e serve como base para muitos outros algoritmos mais complexos. Assim, ao dominar este conceito e a prática em Python, você estará dando um passo gigante na sua jornada no mundo da IA.
Agora é a sua vez! Experimente rodar o código, altere os dados, brinque com os parâmetros e veja os resultados. E, claro, se tiver alguma dúvida ou quiser compartilhar seus experimentos, deixe um comentário aqui embaixo! Adoro ver vocês programando e aprendendo junto comigo! 😊
Até a próxima, e continue explorando o fascinante mundo da IA com Python! 🚀✨

4 comentários em “Seu primeiro algoritmo de IA em Python: Regressão linear na prática”