Olá, entusiastas da programação! Sejam bem-vindos a mais um post do nosso blog, onde vamos mergulhar, primeiramente, no fascinante mundo dos algoritmos de ordenação em Java. Preparados para organizar suas ideias e seus dados? 😜
Neste post, vamos explorar os principais algoritmos de ordenação em Java, com um toque especial: visualizações gráficas animadas! Veremos como cada algoritmo funciona passo a passo, tornando o aprendizado mais intuitivo e divertido. Além disso, forneceremos o código completo para você implementar e experimentar por conta própria.
Por que estudar algoritmos de ordenação?
Dominar algoritmos de ordenação é crucial para qualquer programador, pois eles são a base de muitas operações computacionais. Uma boa escolha de algoritmo pode impactar significativamente a performance da sua aplicação, especialmente ao lidar com grandes volumes de dados.
Os algoritmos que iremos explorar
- Bubble Sort: O clássico “troca-troca” que você ama (ou odeia).
- Selection Sort: Encontre o menor e coloque-o no lugar certo.
- Insertion Sort: Construindo a ordenação elemento por elemento.
- Merge Sort: Dividir para conquistar, mas com elegância.
- Quick Sort: O mestre da eficiência (quando bem implementado).
A mágica da visualização
Para cada algoritmo, criaremos uma visualização gráfica usando Java Swing. Cada barra representará um elemento do array, e sua altura indicará o valor. A animação mostrará as trocas e comparações, permitindo que você visualize o algoritmo em ação.
Implementação completa
Vamos ao código! Afinal, a prática leva à perfeição. A estrutura básica para a visualização será a seguinte:
Classe SortingVisualizer
import javax.swing.*;
import java.awt.*;
import java.util.Random;
import java.util.concurrent.CompletableFuture;
public class SortingVisualizer extends JFrame {
private int[] array;
private VisualPanel panel;
private int delay = 10; // Velocidade da animação
private JComboBox<String> algorithmSelector;
private JButton sortButton;
public SortingVisualizer(int size) {
setTitle("Visualização de Algoritmos de Ordenação");
setSize(800, 650); // Altura aumentada para acomodar os controles
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setLocationRelativeTo(null);
array = generateRandomArray(size);
panel = new VisualPanel(array);
add(panel, BorderLayout.CENTER);
// Painel para os controles
JPanel controlPanel = new JPanel();
algorithmSelector = new JComboBox<>(new String[]{"Bubble Sort", "Selection Sort", "Insertion Sort", "Merge Sort", "Quick Sort"});
sortButton = new JButton("Ordenar");
controlPanel.add(algorithmSelector);
controlPanel.add(sortButton);
add(controlPanel, BorderLayout.SOUTH);
sortButton.addActionListener(e -> startSorting()); // Lidar com o clique no botão
setVisible(true);
}
private void startSorting() {
// Crie uma cópia do array original antes de ordenar
int[] arrayCopy = array.clone();
// Use CompletableFuture para executar a ordenação em uma thread separada
CompletableFuture.runAsync(() -> {
try {
String selectedAlgorithm = (String) algorithmSelector.getSelectedItem();
switch (selectedAlgorithm) {
case "Bubble Sort":
bubbleSort(arrayCopy);
break;
case "Selection Sort":
selectionSort(arrayCopy);
break;
case "Insertion Sort":
insertionSort(arrayCopy);
break;
case "Merge Sort":
mergeSort(arrayCopy);
break;
case "Quick Sort":
quickSort(arrayCopy);
break;
default:
JOptionPane.showMessageDialog(this, "Algoritmo inválido!");
return;
}
panel.setArray(arrayCopy); // Atualiza o array original após a ordenação
panel.repaint();
panel.setHighlightedIndices(-1,-1);
} catch (Exception ex) {
ex.printStackTrace();
} finally {
}
});
}
private int[] generateRandomArray(int size) {
int[] arr = new int[size];
Random random = new Random();
for (int i = 0; i < size; i++) {
arr[i] = random.nextInt(500) + 50; // Valores entre 50 e 550
}
return arr;
}
// Método para trocar dois elementos do array (útil para todos os algoritmos)
private void swap(int[] arr, int i, int j) { // Agora recebe o array como argumento
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
panel.setHighlightedIndices(i, j);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
}
// Pausa para a animação
private void delay() {
try {
Thread.sleep(delay);
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
// Métodos de Ordenação (a serem implementados abaixo)
public void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1])
swap(arr, j, j + 1);
}
}
}
public void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex])
minIndex = j;
}
if (minIndex != i)
swap(arr, i, minIndex);
}
}
public void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
panel.setHighlightedIndices(j, j + 1);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
j = j - 1;
}
arr[j + 1] = key;
}
panel.setArray(arr); // Garante que o array final seja refletido na visualização
panel.repaint();
delay();
}
public void mergeSort(int[] arr) {
mergeSort(arr, 0, arr.length - 1);
}
private void mergeSort(int[] arr, int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
private void merge(int[] arr, int l, int m, int r) {
int n1 = m - l + 1;
int n2 = r - m;
int[] L = new int[n1];
int[] R = new int[n2];
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
panel.setHighlightedIndices(l,r);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
k++;
}
while (i < n1) {
arr[k] = L[i];
panel.setHighlightedIndices(l,r);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
panel.setHighlightedIndices(l,r);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
j++;
k++;
}
}
public void quickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
private void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
private int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
panel.setHighlightedIndices(low, high);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
}
}
swap(arr, i + 1, high);
panel.setHighlightedIndices(low, high);
panel.setArray(arr); // Passa a cópia atualizada do array para o painel
panel.repaint();
delay();
return (i + 1);
}
public static void main(String[] args) {
SwingUtilities.invokeLater(() -> {
new SortingVisualizer(100);
});
}
}Classe VisualPanel
import java.awt.*;
import javax.swing.JPanel;
class VisualPanel extends JPanel {
private int[] array;
private int iHighlight = -1;
private int jHighlight = -1;
public VisualPanel(int[] array) {
this.array = array;
}
public void setHighlightedIndices(int i, int j) {
this.iHighlight = i;
this.jHighlight = j;
}
public void setArray(int[] array) {
this.array = array;
}
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
Graphics2D g2d = (Graphics2D) g;
int width = getWidth() / array.length;
for (int i = 0; i < array.length; i++) {
int height = array[i];
int x = i * width;
int y = getHeight() - height - 50; // Subtrai 50 para dar espaço aos controles
if (i == iHighlight || i == jHighlight) {
g2d.setColor(Color.RED);
} else {
g2d.setColor(Color.BLUE);
}
g2d.fillRect(x, y, width, height);
g2d.setColor(Color.BLACK);
g2d.drawRect(x, y, width, height);
}
iHighlight = -1;
jHighlight = -1;
}
}Funcionamento dos algoritmos
- Bubble Sort: O Bubble Sort é o mais simples de entender. Em primeiro lugar, ele compara elementos adjacentes e os troca se estiverem fora de ordem. Ele repete isso várias vezes até que todo o array esteja ordenado. Em suma, ele “borbulha” os maiores elementos para o final.
- Selection Sort: O Selection Sort, analogamente, encontra o menor elemento no array não ordenado e o troca com o primeiro elemento não ordenado. Ele repete este processo para cada posição do array. Assim, a cada iteração, um elemento é colocado em sua posição correta.
- Insertion Sort: O Insertion Sort, conforme o nome sugere, itera sobre o array e “insere” cada elemento na posição correta em relação aos elementos já ordenados. Isto é, ele constrói o array ordenado um elemento por vez.
- Merge Sort: O Merge Sort adota a estratégia “dividir para conquistar”. Antes de tudo, ele divide o array em metades menores, ordena cada metade recursivamente e, em seguida, mescla as metades ordenadas. A chave é a eficiente função de mesclagem que combina duas metades ordenadas em um único array ordenado.
- Quick Sort: O Quick Sort, sobretudo, escolhe um elemento como “pivô” e particiona o array em duas sub-arrays: elementos menores que o pivô e elementos maiores que o pivô. Ele então ordena as sub-arrays recursivamente. A escolha do pivô impacta drasticamente a performance, mas uma implementação cuidadosa garante alta eficiência.
Como executar
- Compile o código: javac SortingVisualizer.java.
- Execute o código: java SortingVisualizer.
- Selecione um algoritmo na caixa de seleção.
- Clique no botão “Ordenar”.
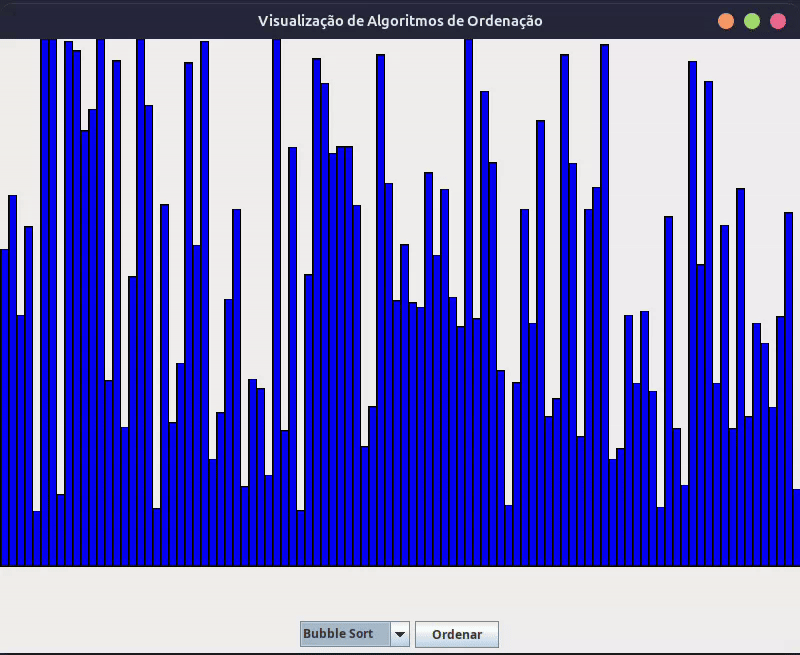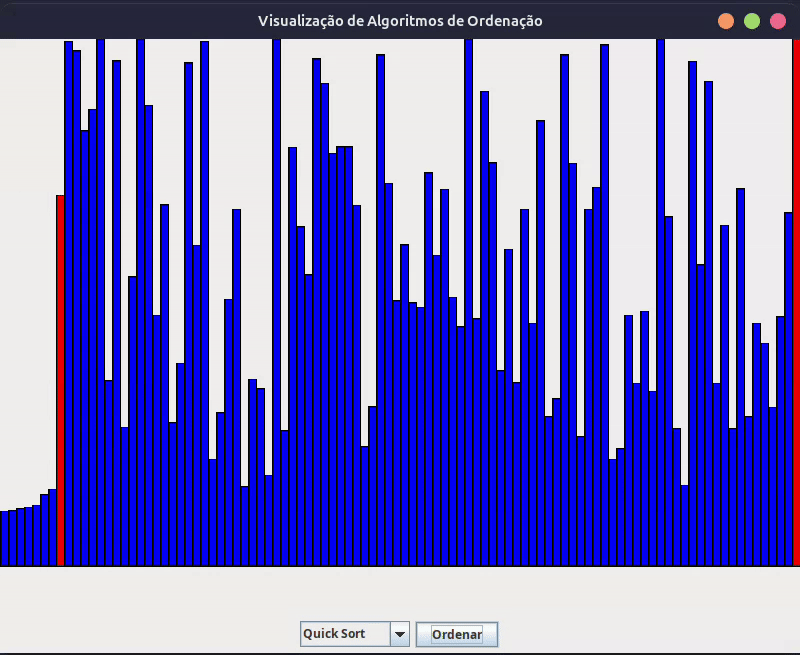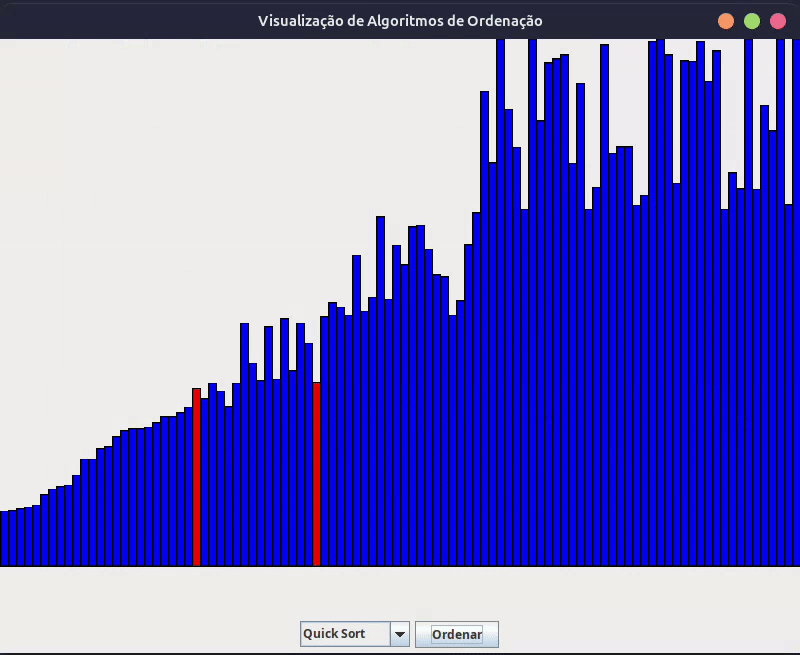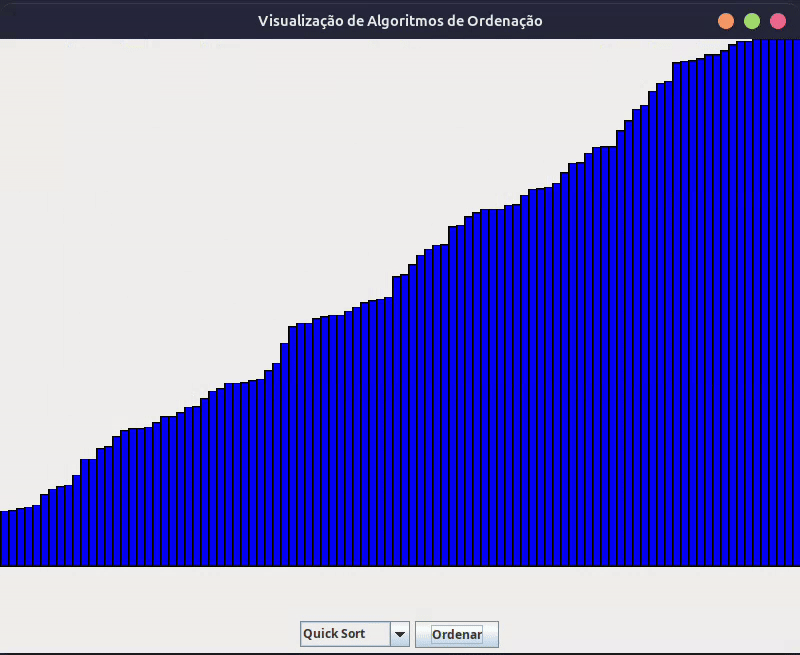
Então, com este guia completo, você tem o poder de visualizar e entender os principais algoritmos de ordenação Java. A combinação de visualização gráfica e implementação prática torna o aprendizado mais eficiente e agradável. Agora, experimente!