No post anterior, desmistificamos a Inteligência Artificial e preparamos nosso ambiente Java para essa jornada emocionante. Agora, chegou o momento de colocarmos a mão na massa e construir nosso primeiro algoritmo de Machine Learning em Java! E para tornar a experiência ainda mais divertida e didática, vamos resolver um problema de classificação bem visual e intuitivo: identificar se um emoji expressa uma emoção positiva ou negativa utilizando Regressão Logística.
“Regressão Logística”? 🤔 Pode soar um pouco complexo, mas, vamos desmistificar esse algoritmo juntos e mostrar como ele pode ser implementado em Java de maneira simples e eficaz. Assim, prepare-se para ver a IA em ação, classificando emojis e aprendendo de forma prática!
Regressão logística: Entendendo o básico de maneira prática 🤓
A Regressão Logística é um algoritmo de classificação, isto é, ele serve para categorizar itens em diferentes classes. No nosso caso, as classes serão “emoji positivo” e “emoji negativo”. Você pode estar se perguntando: “Como um algoritmo matemático consegue classificar emojis?” 🤔 Essa é uma ótima pergunta!
Primeiramente, a Regressão Logística se baseia na ideia de encontrar uma “linha de decisão” que separa as diferentes classes. Imagine um gráfico com emojis espalhados. A Regressão Logística busca traçar uma linha (em problemas mais complexos, pode ser um hiperplano em múltiplas dimensões) que melhor divide os emojis positivos de um lado e os negativos do outro.
Para entender melhor, vamos usar uma analogia. Imagine que você quer separar maçãs de laranjas em uma esteira. Você pode usar características como cor e peso. Maçãs geralmente são mais vermelhas e possuem um certo peso, enquanto laranjas são mais laranjas e têm outro peso. A Regressão Logística faz algo parecido: ela analisa as “características” dos emojis (no nosso caso, simplificaremos ao máximo) e aprende a “linha divisória” entre emojis positivos e negativos.
Em termos mais técnicos (mas ainda simples!):
- É um algoritmo de aprendizado supervisionado: Isso significa que precisamos fornecer exemplos rotulados para o algoritmo aprender. No nosso caso, emojis com seus rótulos (“positivo” ou “negativo”).
- Utiliza a função sigmoide: Essa função transforma a saída do algoritmo em uma probabilidade entre 0 e 1. Probabilidade próxima de 1 indica alta chance de ser “emoji positivo”, próxima de 0, alta chance de ser “emoji negativo”. Valores próximos de 0.5 sugerem maior incerteza.
- Aprende os pesos dos atributos: A Regressão Logística ajusta “pesos” para cada característica (em nosso exemplo, simplificado). Esses pesos determinam a importância de cada característica na decisão final de classificação.
Em resumo, a Regressão Logística é um algoritmo poderoso e relativamente simples para problemas de classificação binária (duas classes), como o nosso de emojis positivos e negativos! E a melhor parte? Vamos implementá-lo em Java agora mesmo! 🚀
Preparando os dados: Emojis como matéria-prima 🍎📊
“Dados são o novo petróleo” – você certamente já ouviu essa frase. E em Inteligência Artificial, ela é totalmente verdadeira! Assim sendo, antes de iniciarmos a programação do algoritmo, precisamos preparar nossos “dados”: os emojis que utilizaremos para treinar e testar nosso classificador.
Para simplificar ao máximo neste primeiro exemplo, vamos criar um conjunto de dados bem pequeno e manual. Dessa forma, o foco estará na lógica do algoritmo em Java sem nos preocuparmos com datasets complexos por enquanto.
Vamos definir uma lista de emojis e seus respectivos rótulos (positivo ou negativo). Poderíamos representar isso em Java como um Map (chave-valor), onde a chave é o emoji (String) e o valor é o rótulo (String também, “positivo” ou “negativo”).
import java.util.HashMap;
import java.util.Map;
public class EmojiSentimentData {
public static Map<String, String> getEmojiSentimentMap() {
Map<String, String> emojiSentimentMap = new HashMap<>();
// Emojis Positivos
emojiSentimentMap.put("😄", "positivo");
emojiSentimentMap.put("😊", "positivo");
emojiSentimentMap.put("😁", "positivo");
emojiSentimentMap.put("😃", "positivo");
emojiSentimentMap.put("😎", "positivo");
emojiSentimentMap.put("👍", "positivo");
emojiSentimentMap.put("🚀", "positivo");
emojiSentimentMap.put("💡", "positivo");
emojiSentimentMap.put("🌟", "positivo");
emojiSentimentMap.put("🎉", "positivo");
// Emojis Negativos
emojiSentimentMap.put("😠", "negativo");
emojiSentimentMap.put("😔", "negativo");
emojiSentimentMap.put("😞", "negativo");
emojiSentimentMap.put("😟", "negativo");
emojiSentimentMap.put("🙁", "negativo");
emojiSentimentMap.put("😨", "negativo");
emojiSentimentMap.put("😩", "negativo");
emojiSentimentMap.put("👎", "negativo");
emojiSentimentMap.put("😭", "negativo");
emojiSentimentMap.put("💔", "negativo");
return emojiSentimentMap;
}
}Neste código:
- Criamos uma classe
EmojiSentimentDatapara organizar nossos dados de emojis. - O método
getEmojiSentimentMap()retorna um HashMap que mapeia emojis (Strings) para seus sentimentos (“positivo” ou “negativo”). - Adicionamos alguns emojis de exemplo para as categorias positiva e negativa. Você pode expandir essa lista com mais emojis!
Por ora, estamos representando os emojis e seus sentimentos de forma textual. No entanto, para a Regressão Logística operar com dados numéricos, precisaríamos transformar esses emojis e rótulos em números. Contudo, para este primeiro exemplo simplificado, vamos focar no algoritmo em si e não na representação complexa de dados. Em posts futuros, exploraremos técnicas mais avançadas de feature engineering (engenharia de características) para representar dados de forma numérica para algoritmos de Machine Learning.
Implementando a regressão logística em Java 💻✍️
Agora que possuímos nossos dados de emojis, vamos para a parte mais empolgante: implementar o algoritmo de Regressão Logística em Java! Importante destacar, para manter este primeiro exemplo didático e focado nos conceitos, implementaremos uma versão simplificada da Regressão Logística, sem otimizações complexas ou frameworks externos (além do ND4J que já configuramos no post anterior para operações matemáticas básicas).
Vamos criar uma classe LogisticRegressionClassifier em Java:
import org.nd4j.linalg.api.buffer.DataType;
import org.nd4j.linalg.api.ndarray.INDArray;
import org.nd4j.linalg.factory.Nd4j;
import org.nd4j.linalg.ops.transforms.Transforms;
import java.util.List;
import java.util.Map;
public class LogisticRegressionClassifier {
private INDArray weights; // Pesos do modelo
private double bias; // Bias (termo de viés)
public LogisticRegressionClassifier(int numFeatures) {
// Inicializa os pesos e o bias (pode ser com valores aleatórios pequenos ou zeros)
this.weights = Nd4j.zeros(DataType.DOUBLE, numFeatures, 1); // Inicializa pesos com zeros e tipo DOUBLE
this.bias = 0.0; // Inicializa bias com zero
}
public double predictProbability(INDArray input) {
// z = (weights^T * x) + bias (combinação linear das features com os pesos + bias)
double z = input.mmul(weights).getDouble(0) + bias; // Usar mmul para multiplicação de matrizes/vetores
// sigmoid(z) = 1 / (1 + exp(-z)) (função sigmoide para transformar z em probabilidade)
return Transforms.sigmoid(Nd4j.scalar(z)).getDouble(0);
}
public String classify(INDArray input, double threshold) {
double probability = predictProbability(input);
if (probability >= threshold) {
return "positivo"; // Se a probabilidade for >= threshold, classifica como "positivo"
} else {
return "negativo"; // Senão, classifica como "negativo"
}
}
public void train(Map<String, String> emojiSentimentMap, int numIterations, double learningRate) {
List<String> emojis = List.copyOf(emojiSentimentMap.keySet()); //Emojis do nosso dataset
for (int iteration = 0; iteration < numIterations; iteration++) {
for (String emoji : emojis) {
String actualSentiment = emojiSentimentMap.get(emoji);
// ***REPRESENTAÇÃO NUMÉRICA SIMPLIFICADA DO EMOJI PARA ESTE EXEMPLO DIDÁTICO***
// Aqui, para este exemplo SUPER SIMPLIFICADO, vamos usar um valor numérico fixo para cada emoji.
// Na prática, teríamos features numéricas reais (e não apenas um número fixo arbitrário).
INDArray inputFeature = Nd4j.create(new double[]{ (double)(emoji.hashCode() % 100) }, new int[]{1, 1}); // Matriz 1x1
double predictionProbability = predictProbability(inputFeature);
String predictedSentiment = classify(inputFeature, 0.5);
int targetLabel = (actualSentiment.equals("positivo")) ? 1 : 0; // 1 para positivo, 0 para negativo
double predictionError = targetLabel - predictionProbability; // Calcula o erro (diferença entre o esperado e o previsto)
// ***AJUSTE RUDIMENTAR DOS PESOS E BIAS (MUITO SIMPLIFICADO - APENAS PARA DEMONSTRAÇÃO)***
// Ajuste dos pesos e bias com base no erro (método incompleto e didático - não é gradiente descendente)
this.weights.addi(inputFeature.transpose().mul(learningRate * predictionError)); // Ajusta os pesos (de forma BEM SIMPLIFICADA)
this.bias = bias + learningRate * predictionError; // Ajusta o bias (de forma BEM SIMPLIFICADA)
if (iteration % 100 == 0 && emojis.indexOf(emoji) == 0 ) {
// Print a cada 100 iterações (e só na primeira vez por iteração externa p/ evitar spam)
System.out.println(
"Iteração " + iteration +
", Emoji: " + emoji +
", Sentimento Real: " + actualSentiment +
", Predição Probabilidade: " + String.format("%.2f", predictionProbability) +
", Predição: " + predictedSentiment +
", Erro: " + String.format("%.2f", predictionError));
}
}
}
}
}Na classe LogisticRegressionClassifier:
- weights: Representa os pesos do nosso modelo de Regressão Logística. É um INDArray (N-Dimensional Array do ND4J), que funciona como uma matriz numérica. numFeatures representa o número de características que usaremos para classificar (neste exemplo simplificado, assumiremos 1 característica por emoji por simplicidade – você pode pensar nisso como um “índice” ou representação numérica simplificada do emoji para este exemplo didático).
- bias: É o termo de viés (bias) da Regressão Logística. Um valor escalar.
- O construtor
LogisticRegressionClassifier(int numFeatures)inicializa os pesos (weights) com zeros e o bias com zero. É importante notar que weights é inicializado comNd4j.zeros(DataType.DOUBLE, numFeatures, 1), definindo explicitamente o tipo de dado como DataType.DOUBLE para evitar problemas de compatibilidade em operações matemáticas.
Agora, vamos detalhar cada método:
Método predictProbability: Função sigmoide e cálculo da probabilidade
Este método calcula a probabilidade de um input (emoji representado numericamente) pertencer à classe “positiva”. Ele utiliza a função sigmoide.
public double predictProbability(INDArray input) {
// z = (weights^T * x) + bias (combinação linear das features com os pesos + bias)
double z = input.mmul(weights).getDouble(0) + bias; // Usar mmul para multiplicação de matrizes/vetores
// sigmoid(z) = 1 / (1 + exp(-z)) (função sigmoide para transformar z em probabilidade)
return Transforms.sigmoid(Nd4j.scalar(z)).getDouble(0);
}Explicação do predictProbability():
- input.mmul(weights): Calcula a multiplicação de matrizes (matrix multiply) entre o input (características do emoji) e os pesos (weights). É crucial usar mmul para multiplicação de matrizes no ND4J.
- .getDouble(0): Extrai o valor escalar do INDArray resultante da multiplicação de matrizes.
- + bias: Adiciona o termo de viés (bias).
- Transforms.sigmoid(Nd4j.scalar(z)): Aplica a função sigmoide ao valor z. Transforms.sigmoid() é uma função do ND4J que calcula a sigmoide elemento a elemento (neste caso, a um escalar).
- .getDouble(0): Extrai o valor da probabilidade (que estará entre 0 e 1) do INDArray resultante da sigmoide.
Método classify: Classificando com base na probabilidade
public String classify(INDArray input, double threshold) {
double probability = predictProbability(input);
if (probability >= threshold) {
return "positivo"; // Se a probabilidade for >= threshold, classifica como "positivo"
} else {
return "negativo"; // Senão, classifica como "negativo"
}
}Explicação do classify():
- predictProbability(input): Chama o método que calculamos anteriormente para obter a probabilidade de ser “positivo”.
- threshold: É o limiar (valor de corte). Se a probabilidade for maior ou igual a este valor, classificamos como “positivo”, caso contrário, como “negativo”. Um valor de threshold comum é 0.5 (classifica como positivo se a probabilidade for >= 0.5).
Método de treinamento simplificado
Implementar um treinamento completo de Regressão Logística (com Gradiente Descendente, por exemplo) seria um pouco complexo para este segundo post introdutório. Para simplificar e focar na ideia principal, criamos um método de treinamento bem rudimentar e ilustrativo, que itera sobre os emojis e “ajusta” os pesos e bias manualmente com base no erro da classificação. É importante frisar que este método NÃO representa um treinamento correto de Regressão Logística, mas serve para demonstrar a ideia de ajuste de parâmetros. Em posts futuros, implementaremos o treinamento correto com Gradiente Descendente.
public void train(Map<String, String> emojiSentimentMap, int numIterations, double learningRate) {
List<String> emojis = List.copyOf(emojiSentimentMap.keySet()); //Emojis do nosso dataset
for (int iteration = 0; iteration < numIterations; iteration++) {
for (String emoji : emojis) {
String actualSentiment = emojiSentimentMap.get(emoji);
// ***REPRESENTAÇÃO NUMÉRICA SIMPLIFICADA DO EMOJI PARA ESTE EXEMPLO DIDÁTICO***
// Aqui, para este exemplo SUPER SIMPLIFICADO, vamos usar um valor numérico fixo para cada emoji.
// Na prática, teríamos features numéricas reais (e não apenas um número fixo arbitrário).
INDArray inputFeature = Nd4j.create(new double[]{ (double)(emoji.hashCode() % 100) }, new int[]{1, 1}); // Matriz 1x1
double predictionProbability = predictProbability(inputFeature);
String predictedSentiment = classify(inputFeature, 0.5);
int targetLabel = (actualSentiment.equals("positivo")) ? 1 : 0; // 1 para positivo, 0 para negativo
double predictionError = targetLabel - predictionProbability; // Calcula o erro (diferença entre o esperado e o previsto)
// ***AJUSTE RUDIMENTAR DOS PESOS E BIAS (MUITO SIMPLIFICADO - APENAS PARA DEMONSTRAÇÃO)***
// Ajuste dos pesos e bias com base no erro (método incompleto e didático - não é gradiente descendente)
this.weights.addi(inputFeature.transpose().mul(learningRate * predictionError)); // Ajusta os pesos (de forma BEM SIMPLIFICADA)
this.bias = bias + learningRate * predictionError; // Ajusta o bias (de forma BEM SIMPLIFICADA)
if (iteration % 100 == 0 && emojis.indexOf(emoji) == 0 ) {
// Print a cada 100 iterações (e só na primeira vez por iteração externa p/ evitar spam)
System.out.println(
"Iteração " + iteration +
", Emoji: " + emoji +
", Sentimento Real: " + actualSentiment +
", Predição Probabilidade: " + String.format("%.2f", predictionProbability) +
", Predição: " + predictedSentiment +
", Erro: " + String.format("%.2f", predictionError));
}
}
}
}Explicação do train() (método de treinamento SUPER SIMPLIFICADO):
- emojiSentimentMap: Nosso dataset de emojis e sentimentos.
- numIterations: Número de vezes que vamos iterar sobre os dados para “ajustar” o modelo. Neste método simplificado, o conceito de iteração serve apenas para ilustrar a ideia de ajuste repetitivo.
- learningRate: Taxa de aprendizado. Controla o “passo” do ajuste dos pesos e bias a cada iteração. No nosso método simplificado, a taxa de aprendizado é utilizada de maneira rudimentar, apenas para influenciar a magnitude do ajuste.
- Representação Numérica Simplificada (inputFeature = Nd4j.create(new double[]{ (double)(emoji.hashCode() % 100) }, new int[]{1, 1})): ATENÇÃO! ESTA PARTE É EXTREMAMENTE SIMPLIFICADA PARA FINS DIDÁTICOS. Na prática, você precisaria de features numéricas significativas para cada emoji (por exemplo, características visuais, contextuais, etc.). Aqui, estamos usando apenas emoji.hashCode() % 100 como um número arbitrário para representar cada emoji, SÓ PARA O CÓDIGO FUNCIONAR DE FORMA SIMPLIFICADA. Não é uma representação útil no mundo real! Criamos inputFeature como uma matriz 1×1 usando Nd4j.create(new double[]{ … }, new int[]{1, 1}) para garantir a compatibilidade com as operações de multiplicação de matrizes (mmul) do ND4J, mesmo sendo apenas uma “feature” por emoji neste exemplo.
- predictProbability(inputFeature) e classify(inputFeature, 0.5): Usamos os métodos que já criamos para obter a predição atual do modelo para o emoji.
- targetLabel: Define o rótulo correto (1 para “positivo”, 0 para “negativo”).
- predictionError: Calcula o erro, que é a diferença entre o rótulo correto e a probabilidade predita.
- Ajuste Rudimentar de Pesos e Bias (this.weights.addi(…) e this.bias = …): ATENÇÃO! ESTE É UM AJUSTE EXTREMAMENTE SIMPLIFICADO E DIDÁTICO! NÃO É O GRADIENTE DESCENDENTE CORRETO DA REGRESSÃO LOGÍSTICA! Estamos apenas “movendo” os pesos e o bias um pouco na direção do erro, multiplicando pelo learningRate. Na Regressão Logística real, o ajuste é feito com base no gradiente da função de custo, utilizando Gradiente Descendente ou algoritmos similares. Aqui, o objetivo é demonstrar a ideia de que o modelo ajusta seus parâmetros com base no erro.
- System.out.println(…): Imprime informações de progresso a cada 100 iterações (e apenas uma vez por iteração externa para não “spamar” o console).
Testando o classificador de emojis! 🧪😄😠
Agora que implementamos as classes EmojiSentimentData e LogisticRegressionClassifier, vamos criar uma classe principal (Main.java, por exemplo) para utilizar e testar nosso classificador de emojis!
import java.util.Map;
import org.nd4j.linalg.api.ndarray.INDArray;
import org.nd4j.linalg.factory.Nd4j;
public class Main {
public static void main(String[] args) {
Map<String, String> emojiSentimentMap = EmojiSentimentData.getEmojiSentimentMap();
// Criando o classificador LogisticRegressionClassifier (1 feature simplificada por emoji)
LogisticRegressionClassifier classifier = new LogisticRegressionClassifier(1);
System.out.println("--- Treinamento do Classificador (SIMPLIFICADO) ---");
classifier.train(emojiSentimentMap, 1000, 0.1); // Treina por 1000 iterações, taxa de aprendizado 0.1
System.out.println("\n--- Testando o Classificador ---");
// Testando com alguns emojis
testEmoji(classifier, "😄");
testEmoji(classifier, "😠");
testEmoji(classifier, "🚀");
testEmoji(classifier, "💔");
testEmoji(classifier, "🤔"); // Emoji neutro/dúvida - não está no dataset de treinamento!
}
public static void testEmoji(LogisticRegressionClassifier classifier, String emoji) {
INDArray inputFeature = Nd4j.create(new double[]{ (double)(emoji.hashCode() % 100) }, new int[]{1, 1}); // Matriz 1x1
String predictedSentiment = classifier.classify(inputFeature, 0.5);
double probability = classifier.predictProbability(inputFeature);
System.out.println("Emoji: " + emoji + ", Predição: " + predictedSentiment + ", Probabilidade (positivo): " + String.format("%.2f", probability));
}
}Na classe Main.java:
- EmojiSentimentData.getEmojiSentimentMap(): Obtém nosso dataset de emojis.
- LogisticRegressionClassifier classifier = new LogisticRegressionClassifier(1): Cria uma instância do nosso classificador, indicando que estamos utilizando 1 “feature” (na verdade, uma representação numérica muito simplificada para cada emoji).
- classifier.train(emojiSentimentMap, 1000, 0.1): Chama o método de treinamento (simplificado) para “ajustar” o modelo com base nos dados de emojis, por 1000 iterações e com taxa de aprendizado 0.1.
- testEmoji(): Um método auxiliar para testar a classificação de um único emoji. Ele utiliza a mesma representação numérica simplificada do treinamento para o emoji de teste (Nd4j.create(new double[]{ (double)(emoji.hashCode() % 100) }, new int[]{1, 1})), chama o método classify() para obter a predição e imprime o emoji, a predição e a probabilidade.
- No main(), testamos com alguns emojis (😄, 😠, 🚀, 💔) que estão no dataset de treinamento, e também com um emoji novo que não estava no dataset (🤔).
Execute a classe Main.java! Você deverá visualizar a saída do treinamento (as mensagens “Iteração…”) e então os resultados dos testes.
Saída Esperada (Aproximada):
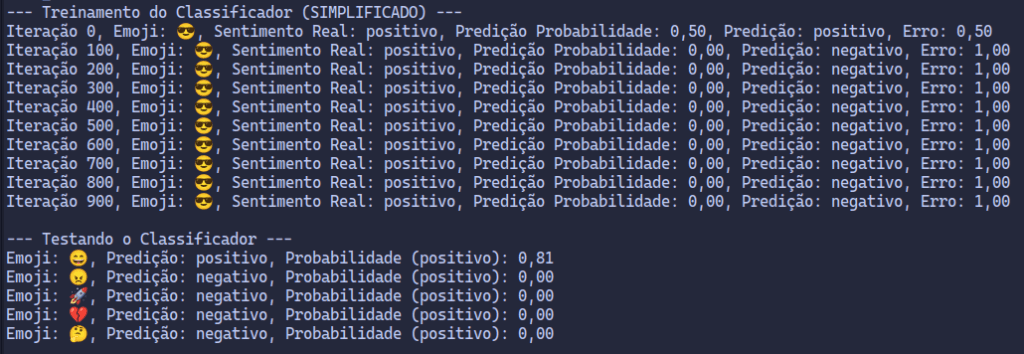
Taxa de erro elevada e aprendizado limitado – Resultados esperados!
Se você executar o código e observar a saída, poderá notar que, mesmo após o “treinamento”, a taxa de erro (representada pela coluna “Erro” durante o treinamento, e implicitamente na qualidade das predições nos testes) permanece relativamente alta, próxima de 1.0. Este resultado é completamente esperado e, na verdade, instrutivo neste exemplo didático!
Existem diversas razões para essa alta taxa de erro e o aprendizado limitado do modelo:
- Método de Treinamento Simplificado: Como já discutido, o método train() que implementamos é extremamente rudimentar e não corresponde ao treinamento real da Regressão Logística com algoritmos de otimização como Gradiente Descendente. Ele serve apenas para demonstrar a ideia de ajuste de parâmetros, mas não otimiza o modelo de forma eficaz.
- Representação Numérica Arbitrária dos Emojis: Utilizamos emoji.hashCode() % 100 como uma forma completamente arbitrária de representar os emojis numericamente. Essa representação não captura nenhuma informação relevante sobre o sentimento ou características visuais dos emojis. É como se o algoritmo estivesse tentando aprender a classificar com base em “números aleatórios” associados a cada emoji. Em problemas reais de PLN e Visão Computacional, a escolha de features (características) relevantes é crucial para o sucesso do modelo.
- Dataset Pequeno e Simplificado: Nosso dataset de apenas 20 emojis é muito pequeno para um algoritmo de Machine Learning aprender padrões robustos e generalizáveis. Modelos de Machine Learning, especialmente algoritmos mais complexos como Redes Neurais, geralmente requerem datasets massivos para um bom aprendizado.
- Ausência de Otimização: Um algoritmo de Regressão Logística “de verdade” utiliza técnicas de otimização para encontrar os melhores valores para os pesos e bias que minimizam o erro no dataset de treinamento. Nosso método simplificado não realiza nenhuma otimização formal.
Em suma, a taxa de erro elevada não indica um problema com o código corrigido. Pelo contrário, ela é uma consequência direta das simplificações didáticas que fizemos para manter este primeiro exemplo acessível e focado nos conceitos básicos.
O propósito didático alcançado!
Mesmo com as limitações e a alta taxa de erro, nós cumprimos com o propósito principal:
- Apresentar a Regressão Logística de forma prática e acessível em Java.
- Guiá-lo na implementação do esqueleto de um classificador de Machine Learning, desde a preparação dos dados até a predição e um conceito simplificado de treinamento.
- Fornecer um exemplo executável em Java, permitindo que você veja a IA “em ação”, mesmo que de forma simplificada e com resultados limitados.
- Estabelecer uma base sólida para os próximos posts da série, onde exploraremos algoritmos mais avançados, datasets mais complexos e técnicas de treinamento mais robustas.
Próximos passos e expandindo seus horizontes de IA em Java… 🚀
Neste post, demos um passo importante e programamos nosso primeiro algoritmo de Machine Learning em Java: um classificador de emojis com Regressão Logística (em sua versão didática e simplificada). Você viu como preparar dados, implementar o algoritmo, “treinar” (de forma simplificada) e testar o modelo.
No próximo post, avançaremos para um problema mais prático e relevante: previsão de preços de imóveis usando Regressão Linear em Java! Trabalharemos com um dataset real de preços de imóveis e construiremos um modelo preditivo completo em Java, aplicando os conceitos de Machine Learning a um problema do mundo real! Prepare-se para mais código, mais aprendizado prático e resultados ainda mais interessantes! 🏠💰
Gostou deste post? Compartilhe com seus amigos desenvolvedores Java que também querem dominar a Inteligência Artificial! Deixe seu comentário abaixo com dúvidas, sugestões e ideias para os próximos posts da série. Vamos construir juntos essa comunidade de IA em Java!💪


2 comentários em “Classificador de Emojis com Regressão Logística em Java! 😄😠”