E aí, pessoal! Tudo na paz por aí? 😎
Nos posts anteriores, exploramos a Regressão Linear para previsões numéricas e a Classificação Inteligente para separar dados em categorias pré-definidas. Agora, vamos dar um passo além e mergulhar em um mundo onde as categorias não são conhecidas de antemão. Preparem-se para dominar o Clustering, a arte de agrupar dados como um mestre e revelar padrões ocultos que ninguém mais vê! 🕵️♀️
Clustering: Desvendando grupos escondidos nos seus dados 🧩
Primeiramente, imagine que você tem uma grande coleção de objetos, como fotos, clientes, músicas ou documentos. Eventualmente, você pode suspeitar que esses objetos se agrupam naturalmente em grupos com características semelhantes, contudo, você não sabe quais são esses grupos nem quantas categorias existem. É exatamente nesse cenário que o Clustering brilha!
Em essência, o Clustering é uma técnica de aprendizado não supervisionado (diferente da classificação e regressão, que são supervisionadas) que busca agrupar dados semelhantes em clusters (grupos), de forma que os dados dentro de um mesmo cluster sejam mais parecidos entre si do que com os dados de outros clusters. Ou seja, o Clustering encontra estrutura e organização em dados aparentemente aleatórios, sem que você precise dizer ao algoritmo quais são essas estruturas.
Para ilustrar, pense em algumas aplicações práticas de Clustering que nos cercam:
- Segmentação de Clientes: Empresas usam Clustering para agrupar clientes com perfis de compra semelhantes, permitindo campanhas de marketing mais direcionadas e eficazes. Por exemplo, um varejista pode identificar grupos de clientes “jovens e modernos”, “famílias tradicionais” ou “consumidores de luxo”.
- Sistemas de Recomendação: Plataformas de streaming de música e vídeo utilizam Clustering para agrupar usuários com gostos similares, recomendando conteúdos que um grupo gosta para outros membros do mesmo grupo.
- Detecção de Anomalias: Clustering pode ajudar a identificar pontos de dados que não se encaixam em nenhum grupo, indicando possíveis anomalias, fraudes ou erros. Imagine, por exemplo, detectar transações bancárias suspeitas que se desviam do padrão de comportamento normal de um cliente.
- Análise de Imagens: Em visão computacional, Clustering pode ser usado para segmentar imagens em regiões com cores ou texturas semelhantes, facilitando a identificação de objetos e padrões visuais.
Algoritmos de Clustering: As ferramentas do mestre do agrupamento 🧰
Assim como em outras áreas da IA, existem diversos algoritmos de Clustering, cada um com suas características e aplicações. Alguns dos mais populares são:
- K-Means: Um dos algoritmos de Clustering mais simples e amplamente utilizados. Em resumo, o K-Means busca particionar os dados em k clusters, onde k é um número pré-definido pelo usuário. Ele faz isso iterativamente, atribuindo cada ponto de dados ao cluster mais próximo e recalculando os centros dos clusters até convergência.
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise): Um algoritmo de Clustering baseado em densidade, que agrupa pontos próximos com alta densidade e marca pontos isolados como ruído. Dessa forma, o DBSCAN é capaz de descobrir clusters de formatos arbitrários e lidar com outliers de forma robusta.
- Hierarchical Clustering: Algoritmos que criam uma hierarquia de clusters, representando os dados em diferentes níveis de granularidade. Existem duas abordagens principais: aglomerativa (começa com cada ponto em seu próprio cluster e os agrupa iterativamente) e divisiva (começa com todos os pontos em um único cluster e o divide recursivamente).
Mão na massa: Agrupando dados de íris com K-Means em Python 🌸
Agora, vamos à prática! Vamos usar novamente o dataset Iris, mas desta vez, vamos aplicar o algoritmo K-Means para agrupar as flores em clusters, sem usar as informações sobre as espécies (afinal, em Clustering, as categorias são desconhecidas!). Vamos ver se o K-Means consegue encontrar grupos que se assemelham às espécies originais.
Importar as dependências
Primeiro passo, importar as bibliotecas essenciais:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score- sklearn.cluster.KMeans: Classe do scikit-learn que implementa o algoritmo K-Means.
- sklearn.metrics.silhouette_score: Métrica para avaliar a qualidade dos clusters formados.
Carregar o dataset
Em seguida, carregar o dataset Iris e preparar os dados:
# Carregar o dataset Iris
iris = load_iris()
X = iris.data # Características das flores (usaremos apenas as features para clustering)
# Definir o número de clusters (vamos tentar 3, pois sabemos que existem 3 espécies de Iris)
num_clusters = 3- X = iris.data: Carregamos apenas as características das flores, pois no Clustering não usamos os rótulos das espécies (que seriam iris.target).
- num_clusters = 3: Definimos o número de clusters para 3, já que sabemos que existem 3 espécies de Iris. Em um problema real, geralmente precisamos experimentar diferentes números de clusters ou usar métodos para estimar o número ideal.
Criar e treinar o modelo
Agora, criar e treinar o modelo K-Means:
# Criar o modelo K-Means
kmeans = KMeans(n_clusters=num_clusters, random_state=42, n_init=10) # n_init para evitar problemas de convergência
# Treinar o modelo com os dados
kmeans.fit(X)- kmeans = KMeans(n_clusters=num_clusters, random_state=42, n_init=10): Cria uma instância do modelo K-Means, definindo o número de clusters (n_clusters=num_clusters) e random_state para reprodutibilidade. n_init=10 executa o K-Means 10 vezes com diferentes inicializações e escolhe a melhor solução, o que ajuda a evitar problemas de convergência em mínimos locais.
- kmeans.fit(X): Treina o modelo K-Means com os dados X. O algoritmo irá iterativamente atribuir os pontos aos clusters e ajustar os centros dos clusters até encontrar uma configuração estável.
Obter os rótulos e os centros
Modelo treinado, podemos obter os rótulos dos clusters atribuídos a cada ponto de dados e os centros dos clusters:
# Obter os rótulos dos clusters e os centros dos clusters
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
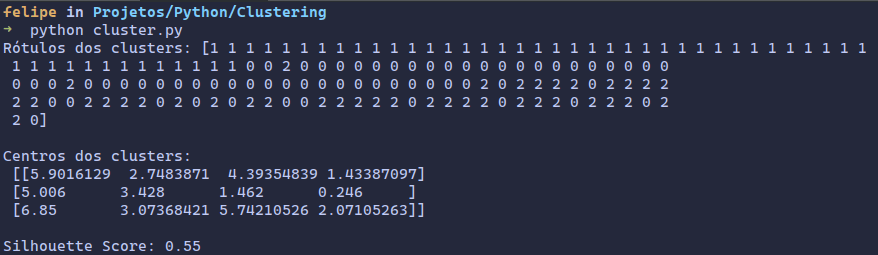
print("Rótulos dos clusters:", labels)
print("\nCentros dos clusters:\n", centroids)- labels = kmeans.labels_: Atribui os rótulos dos clusters encontrados pelo K-Means a cada ponto de dados. labels será um array com o mesmo tamanho de X, onde cada elemento indica o cluster ao qual o ponto correspondente foi atribuído.
- centroids = kmeans.cluster_centers_: Obtém as coordenadas dos centros dos clusters encontrados pelo K-Means.
Visualização gráfica
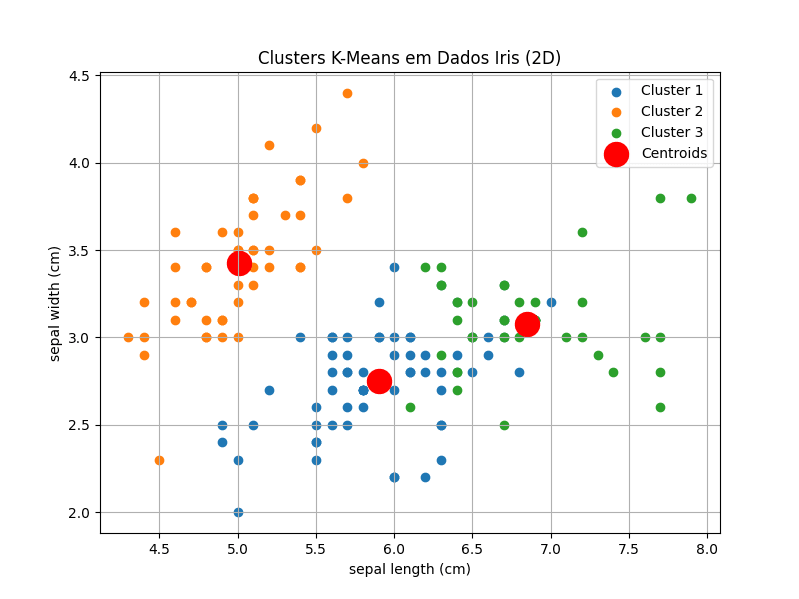
Para visualizar os clusters (limitando a 2 dimensões para facilitar a visualização), vamos usar as duas primeiras características do dataset Iris (sepal length e sepal width) e plotar os pontos de dados coloridos pelos clusters e os centros dos clusters:
# Visualizar os clusters (usando apenas as 2 primeiras features para plotar em 2D)
plt.figure(figsize=(8, 6))
# Plotar os clusters
for i in range(num_clusters):
plt.scatter(X[labels == i, 0], X[labels == i, 1], label=f'Cluster {i+1}') # Pontos de cada cluster
# Plotar os centros dos clusters
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', label='Centroids') # Centros em vermelho e maiores
plt.xlabel(iris.feature_names[0]) # Rótulo do eixo x (sepal length)
plt.ylabel(iris.feature_names[1]) # Rótulo do eixo y (sepal width)
plt.title('Clusters K-Means em Dados Iris (2D)')
plt.legend()
plt.grid(True)
plt.show()- plt.figure(figsize=(8, 6)): Cria uma figura para o gráfico.
- for i in range(num_clusters):: Itera sobre os clusters.
- plt.scatter(…): Plota os pontos de dados do cluster i, usando as duas primeiras características (colunas 0 e 1 de X). A condição labels == i seleciona apenas os pontos pertencentes ao cluster i.
- plt.scatter(centroids[:, 0], centroids[:, 1], …): Plota os centros dos clusters em vermelho e com tamanho maior, usando as duas primeiras coordenadas dos centros (centroids[:, 0] e centroids[:, 1]).
- plt.xlabel(…), plt.ylabel(…), plt.title(…), plt.legend(), plt.grid(True), plt.show(): Configurações do gráfico (rótulos, título, legenda, grade e exibição).
Qualidade do cluster
Para avaliar a qualidade do Clustering, podemos usar o Silhouette Score, que mede o quão bem cada ponto se encaixa no seu cluster em comparação com outros clusters. Valores próximos de 1 indicam um bom Clustering, valores próximos de 0 indicam clusters sobrepostos e valores negativos indicam que os pontos podem ter sido atribuídos ao cluster errado.
# Avaliar a qualidade do clustering com Silhouette Score
silhouette_avg = silhouette_score(X, labels)
print(f"\nSilhouette Score: {silhouette_avg:.2f}")- silhouette_avg = silhouette_score(X, labels): Calcula o Silhouette Score para os clusters encontrados.
- print(…): Imprime o Silhouette Score.
Código completo
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# Carregar o dataset Iris
iris = load_iris()
X = iris.data
# Definir o número de clusters
num_clusters = 3
# Criar o modelo K-Means
kmeans = KMeans(n_clusters=num_clusters, random_state=42, n_init=10)
# Treinar o modelo com os dados
kmeans.fit(X)
# Obter os rótulos dos clusters e os centros dos clusters
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
print("Rótulos dos clusters:", labels)
print("\nCentros dos clusters:\n", centroids)
# Visualizar os clusters (usando apenas as 2 primeiras features para plotar em 2D)
plt.figure(figsize=(8, 6))
for i in range(num_clusters):
plt.scatter(X[labels == i, 0], X[labels == i, 1], label=f'Cluster {i+1}')
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', label='Centroids')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title('Clusters K-Means em Dados Iris (2D)')
plt.legend()
plt.grid(True)
plt.show()
# Avaliar a qualidade do clustering com Silhouette Score
silhouette_avg = silhouette_score(X, labels)
print(f"\nSilhouette Score: {silhouette_avg:.2f}")Execute este código e você verá um gráfico mostrando os clusters encontrados pelo K-Means nos dados Iris (usando as duas primeiras características para visualização 2D), os centros dos clusters e o Silhouette Score para avaliar a qualidade do agrupamento. Desse modo, você terá explorado o poder do Clustering na prática!
Parabéns! Você Se Tornou um Mestre em Agrupamento! 🏆🎉
Em resumo, neste post, você desvendou o conceito de Clustering, aprendeu sobre o algoritmo K-Means e, mais importante, implementou um modelo de Clustering em Python para agrupar dados reais. Agora, você tem as habilidades para aplicar Clustering em seus próprios projetos e descobrir padrões ocultos em seus dados!
Lembre-se, o Clustering é uma ferramenta poderosa para análise exploratória de dados e para diversas aplicações em IA e Ciência de Dados. Portanto, continue praticando, experimentando diferentes algoritmos e datasets, e você se tornará um verdadeiro mestre em agrupar dados!
E aí, pronto para começar a agrupar tudo por aí? Experimente rodar o código, altere o número de clusters, teste outros algoritmos de Clustering (como DBSCAN), explore outros datasets e veja o que você descobre. E não hesite, se tiver dúvidas ou quiser compartilhar suas descobertas, deixe um comentário aqui embaixo! Adoramos aprender e explorar juntos! 😊
Até a próxima, e continue desvendando os segredos dos dados com Python e IA! 🚀✨