Otimização de rotas

Algoritmo genético em Java: Otimizando rotas e o problema do caixeiro viajante

Por

E aí, galera da programação! 👋 Hoje, vamos embarcar em uma aventura que une a beleza da otimização com a praticidade do desenvolvimento Java. Afinal, quem não gosta de ver um problema complexo resolvido com elegância? Vamos criar um programa que resolve o clássico “Problema do Caixeiro Viajante” usando um algoritmo genético, tudo isso com uma interface gráfica feita em Swing. Parece desafiador? Pois acredite, é mais divertido do que você imagina!

Por que o problema do caixeiro viajante?

O “Problema do Caixeiro Viajante” (PCV) é um desafio famoso na ciência da computação. Imagine um vendedor que precisa visitar várias cidades e quer encontrar o caminho mais curto para percorrer todas elas. Ou seja, o PCV busca o circuito de menor distância que passa por todos os pontos dados uma única vez. Esse problema, aparentemente simples, torna-se extremamente complexo à medida que o número de pontos aumenta, sendo classificado como NP-difícil.

E por que algoritmo genético?

Nesse sentido, é que os algoritmos genéticos entram em cena. Eles são inspirados na seleção natural e evolução biológica. Assim, em vez de tentar todas as combinações possíveis (o que seria inviável), o algoritmo genético cria uma “população” de soluções (rotas), simula um processo evolutivo para aprimorar as rotas e ao fim, encontra a melhor rota para nosso caixeiro viajante. É uma abordagem inteligente para problemas de otimização, já que funciona muito bem em problemas complexos como o PCV.

Mão na massa: Implementação em Java com Swing

Vamos ao código! Primeiramente, dividiremos o problema em classes seguindo os princípios SOLID, para deixar tudo organizado e fácil de manter.

Classe Point (representando os pontos)

public class Point {
    private double x;
    private double y;

    public Point(double x, double y) {
        this.x = x;
        this.y = y;
    }

    public double getX() {
        return x;
    }

    public double getY() {
        return y;
    }

    public double distance(Point other) {
        double dx = this.x - other.x;
        double dy = this.y - other.y;
        return Math.sqrt(dx * dx + dy * dy);
    }
}

Classe Path (representando o caminho)

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class Path {
    private List<Point> points;
    private double distance = 0;

    public Path(List<Point> points) {
        this.points = new ArrayList<>(points);
        calculateDistance();
    }

    public void setPoints(List<Point> points) {
        this.points = new ArrayList<>(points);
        calculateDistance();
    }

    public List<Point> getPoints() {
        return points;
    }

    public double getDistance() {
        return distance;
    }

    public void calculateDistance() {
        distance = 0;
        for (int i = 0; i < points.size() - 1; i++) {
            distance += points.get(i).distance(points.get(i + 1));
        }

        distance += points.get(points.size() - 1).distance(points.get(0));
    }


    public void swapPoints(int index1, int index2){
        Collections.swap(points, index1, index2);
        calculateDistance();
    }
}
Ver mais

Classe GeneticAlgorithm (implementando o algoritmo)

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Random;

public class GeneticAlgorithm {
    private int populationSize;
    private double mutationRate;
    private int generations;
    private List<Point> points;
    private Random random;

    public GeneticAlgorithm(List<Point> points, int populationSize, double mutationRate, int generations) {
        this.points = points;
        this.populationSize = populationSize;
        this.mutationRate = mutationRate;
        this.generations = generations;
        this.random = new Random();
    }

    public Path run() {
        List<Path> population = initializePopulation();

        for (int i = 0; i < generations; i++) {
            population = evolvePopulation(population);
        }

        population.sort(Comparator.comparingDouble(Path::getDistance));

        return population.get(0);
    }

    private List<Path> initializePopulation() {
        List<Path> population = new ArrayList<>();

        for (int i = 0; i < populationSize; i++) {
            List<Point> shuffledPoints = new ArrayList<>(points);
            Collections.shuffle(shuffledPoints, random);
            population.add(new Path(shuffledPoints));
        }

        return population;
    }

    private List<Path> evolvePopulation(List<Path> population) {
        List<Path> nextGeneration = new ArrayList<>();

        population.sort(Comparator.comparingDouble(Path::getDistance));

        for (int i = 0; i < populationSize / 2 ; i++) {
            nextGeneration.add(population.get(i));
        }

        while(nextGeneration.size() < populationSize) {
            int index1 = random.nextInt(populationSize/2);
            int index2 = random.nextInt(populationSize/2);

            Path parent1 = population.get(index1);
            Path parent2 = population.get(index2);

            Path child = crossover(parent1, parent2);

            mutate(child);

            nextGeneration.add(child);
        }

        return nextGeneration;
    }

    private Path crossover(Path parent1, Path parent2) {
        List<Point> childPoints = new ArrayList<>();

        int start = random.nextInt(parent1.getPoints().size());
        int end = random.nextInt(parent1.getPoints().size());

        if (start > end) {
            int temp = start;
            start = end;
            end = temp;
        }

        for (int i = start; i <= end; i++) {
            childPoints.add(parent1.getPoints().get(i));
        }

        for (Point point : parent2.getPoints()) {
            if (!childPoints.contains(point)) {
                childPoints.add(point);
            }
        }

        return new Path(childPoints);
    }


    private void mutate(Path path){
        if (random.nextDouble() < mutationRate) {
            int index1 = random.nextInt(path.getPoints().size());
            int index2 = random.nextInt(path.getPoints().size());
            path.swapPoints(index1, index2);
        }
    }
}
Ver mais

A classe GeneticAlgorithm é a responsável por encapsular a lógica do algoritmo genético para resolver o Problema do Caixeiro Viajante (PCV). Ela é o motor que cria, evolui e encontra a melhor rota através de um processo de “seleção natural” simulado.

Atributos Principais

  1. populationSize: Um inteiro que define o tamanho da população, ou seja, quantas rotas (caminhos) serão consideradas em cada geração. Uma população maior pode explorar mais soluções, mas também aumenta o custo computacional.
  2. mutationRate: Um valor double (entre 0 e 1) que determina a probabilidade de ocorrer mutação em um indivíduo. A mutação é uma pequena alteração aleatória que pode gerar diversidade na população, evitando que ela fique presa em soluções subótimas.
  3. generations: Um inteiro que define quantas gerações o algoritmo genético irá rodar. Quanto mais gerações, mais tempo o algoritmo terá para evoluir e encontrar melhores soluções.
  4. points: Uma lista de objetos Point que representam as cidades que precisam ser visitadas.
  5. random: Um objeto da classe Random, utilizado para geração de números aleatórios.

Métodos Chave

  1. public Path run():
    • Propósito: Este é o método que inicia e executa todo o processo do algoritmo genético.
    • Funcionamento:
      • Ele primeiro chama initializePopulation() para criar a população inicial de rotas.
      • Em seguida, ele itera através das gerações (for (int i = 0; i < generations; i++)). Em cada geração:
        • A função evolvePopulation é chamada, simulando a reprodução e evolução da população.
      • Finalmente, ele ordena a população pelo custo (distância) e retorna a melhor rota encontrada.
  2. private List<Path> initializePopulation():
    • Propósito: Cria a população inicial de rotas de forma aleatória.
    • Funcionamento:
      • Para cada indivíduo da população, ele cria uma lista de Point e aleatoriamente embaralha a ordem dos pontos e armazena dentro do objeto Path.
      • Essas rotas aleatórias representam os primeiros indivíduos (caminhos) que serão avaliados pelo algoritmo genético.
  3. private List<Path> evolvePopulation(List<Path> population):
    • Propósito: Simula a evolução da população atual para a próxima geração.
    • Funcionamento:
      • Primeiro, ordena a população atual de rotas, com base na sua distância total (do melhor para o pior).
      • Então, seleciona a metade melhor da população (os “pais”).
      • Depois, cria uma nova geração usando reprodução.
      • Para cada filho, executa crossover (recombinação) com pais diferentes.
      • A mutação pode ser aplicada no indivíduo filho de forma aleatória.
      • O método continua este processo até que o tamanho da nova população seja o mesmo da população anterior.
  4. private Path crossover(Path parent1, Path parent2):
    • Propósito: Combina material genético (rotas) de dois pais para criar um filho (nova rota).
    • Funcionamento:
      • Escolhe um intervalo aleatório de pontos do primeiro pai.
      • Adiciona esse intervalo ao filho.
      • Adiciona os pontos restantes do segundo pai, mantendo a ordem original.
      • Retorna um novo objeto Path (o filho).
  5. private void mutate(Path path):
    • Propósito: Aplica uma mutação a uma rota com uma determinada probabilidade (determinada pelo mutationRate).
    • Funcionamento:
      • Verifica a probabilidade do path atual sofrer mutação
      • Se a probabilidade for alta, a mutação troca a posição de dois pontos do caminho de forma aleatória.

Entendendo a Lógica do Algoritmo Genético na Classe

A ideia principal é criar uma “população” de soluções (rotas) aleatórias, avaliá-las (pela distância total), e fazer com que as soluções melhores se reproduzam (através do crossover) e sofram pequenas alterações (através da mutação), ao longo de várias gerações. Dessa forma, o algoritmo tenta convergir para a melhor solução possível sem ter que avaliar todos os caminhos possíveis.

  • Inicialização: Criar rotas aleatórias para começar o processo evolutivo.
  • Seleção: Escolher as rotas de melhor desempenho para se reproduzirem.
  • Crossover: Criar novos caminhos, combinando informações de caminhos existentes.
  • Mutação: Introduzir variedade nas rotas, evitando que o algoritmo fique preso em soluções ruins.
  • Iteração: Repetir esse processo por várias gerações até encontrar uma solução que seja satisfatória.

Em resumo, a classe GeneticAlgorithm encapsula a inteligência do algoritmo genético, guiando a busca pela melhor rota através da simulação de um processo evolutivo. Cada método dentro dessa classe tem um propósito claro e bem definido para fazer essa busca funcionar de forma eficaz.

Classe Main (Interface Swing)

import javax.swing.*;
import java.awt.*;
import java.awt.event.ActionEvent;
import java.awt.geom.Ellipse2D;
import java.awt.geom.Line2D;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;

public class Main extends JFrame {
    private static final int WIDTH = 800;
    private static final int HEIGHT = 600;
    private static final int POINT_SIZE = 10;
    private static final double MUTATION_RATE = 0.01;
    private static final int POPULATION_SIZE = 100;
    private static final int GENERATIONS = 500;

    private JPanel panel;
    private JButton generatePointsButton;
    private JButton findPathButton;
    private JTextField numberOfPointsField;
    private List<Point> points;
    private Path bestPath;

    public Main() {
        setTitle("Problema do Caixeiro Viajante");
        setSize(WIDTH, HEIGHT);
        setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
        setLocationRelativeTo(null);
        setLayout(null);

        initComponents();
    }

    private void initComponents() {
        panel = new JPanel(){
            @Override
            protected void paintComponent(Graphics g) {
                super.paintComponent(g);
                drawPoints(g);
                if(bestPath != null){
                    drawPath(g);
                }

            }
        };

        panel.setLayout(null);
        panel.setBackground(Color.WHITE);
        panel.setBounds(0,100,WIDTH,HEIGHT-100);
        add(panel);

        numberOfPointsField = new JTextField("5");
        numberOfPointsField.setBounds(10, 20, 50, 30);
        add(numberOfPointsField);

        generatePointsButton = new JButton("Gerar Pontos");
        generatePointsButton.setBounds(70, 20, 120, 30);
        generatePointsButton.addActionListener(this::generatePoints);
        add(generatePointsButton);

        findPathButton = new JButton("Encontrar Melhor Rota");
        findPathButton.setBounds(200, 20, 170, 30);
        findPathButton.addActionListener(this::findBestPath);
        add(findPathButton);
    }

    private void generatePoints(ActionEvent e) {
        points = new ArrayList<>();
        int numberOfPoints =  Integer.parseInt(numberOfPointsField.getText());
        Random random = new Random();

        for (int i = 0; i < numberOfPoints; i++) {
            double x = random.nextDouble() * (WIDTH - POINT_SIZE);
            double y = random.nextDouble() * (HEIGHT - 100 - POINT_SIZE);
            points.add(new Point(x,y));
        }

        bestPath = null;
        panel.repaint();
    }

    private void findBestPath(ActionEvent e) {
        if (points == null || points.isEmpty())
            return;

        GeneticAlgorithm ga = new GeneticAlgorithm(points, POPULATION_SIZE, MUTATION_RATE, GENERATIONS);
        bestPath = ga.run();

        new Thread(() -> {
            animatePath();
        }).start();
    }

    private void animatePath() {
        List<Point> pathPoints = bestPath.getPoints();

        for (int i = 0; i < pathPoints.size() - 1; i++) {
            bestPath.setPoints(pathPoints.subList(0, i + 2));
            panel.repaint();

            try {
                Thread.sleep(200);
            } catch (InterruptedException e) {
                Thread.currentThread().interrupt();
                return;
            }
        }

        bestPath.setPoints(pathPoints);
        panel.repaint();
    }

    private void drawPoints(Graphics g) {
        Graphics2D g2d = (Graphics2D) g;
        if (points != null) {
            g2d.setColor(Color.BLACK);
            for (Point point : points) {
                Ellipse2D circle = new Ellipse2D.Double(point.getX(), point.getY(), POINT_SIZE, POINT_SIZE);
                g2d.fill(circle);
            }
        }
    }

    private void drawPath(Graphics g){
        if (bestPath != null) {
            Graphics2D g2d = (Graphics2D) g;
            g2d.setColor(Color.RED);
            List<Point> pathPoints = bestPath.getPoints();

            for(int i = 0; i < pathPoints.size() - 1; i++) {
                Point p1 = pathPoints.get(i);
                Point p2 = pathPoints.get(i + 1);
                Line2D line = new Line2D.Double(p1.getX() + POINT_SIZE/2 , p1.getY()+ POINT_SIZE/2 , p2.getX() + POINT_SIZE/2 , p2.getY() + POINT_SIZE/2);
                g2d.draw(line);
            }

            Point p1 = pathPoints.get(pathPoints.size() - 1);
            Point p2 = pathPoints.get(0);
            Line2D line = new Line2D.Double(p1.getX() + POINT_SIZE/2 , p1.getY()+ POINT_SIZE/2 , p2.getX() + POINT_SIZE/2 , p2.getY() + POINT_SIZE/2);
            g2d.draw(line);
        }
    }

    public static void main(String[] args) {
        SwingUtilities.invokeLater(() -> new Main().setVisible(true));
    }
}
Ver mais

O que cada parte faz

  • Point: Representa um ponto com coordenadas x e y.
  • Path: Representa um caminho, um sequência de pontos e sua distância total.
  • GeneticAlgorithm: Implementa o algoritmo genético, com métodos para inicializar a população, evoluir através das gerações e calcular a aptidão dos indivíduos.
  • Main: A classe principal, cria a interface gráfica usando Swing e orquestra o algoritmo genético.

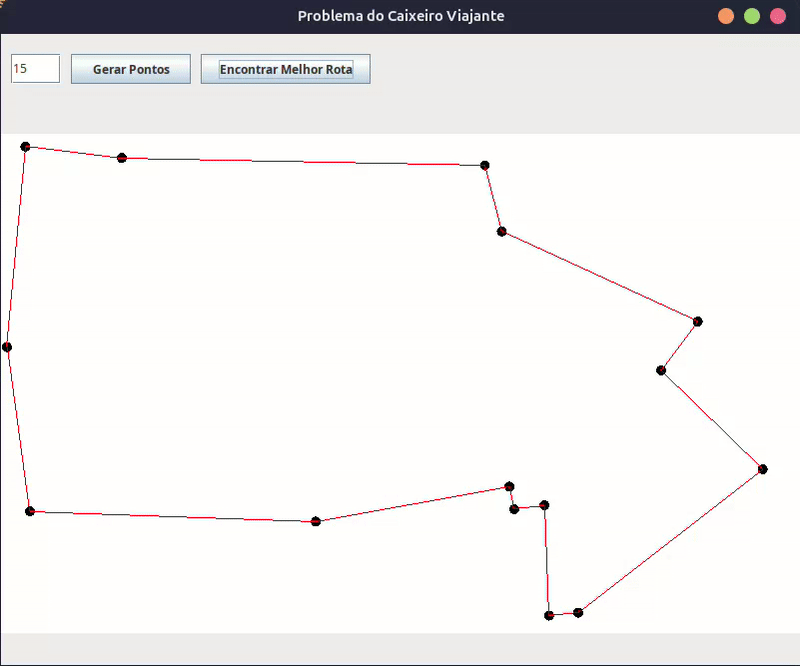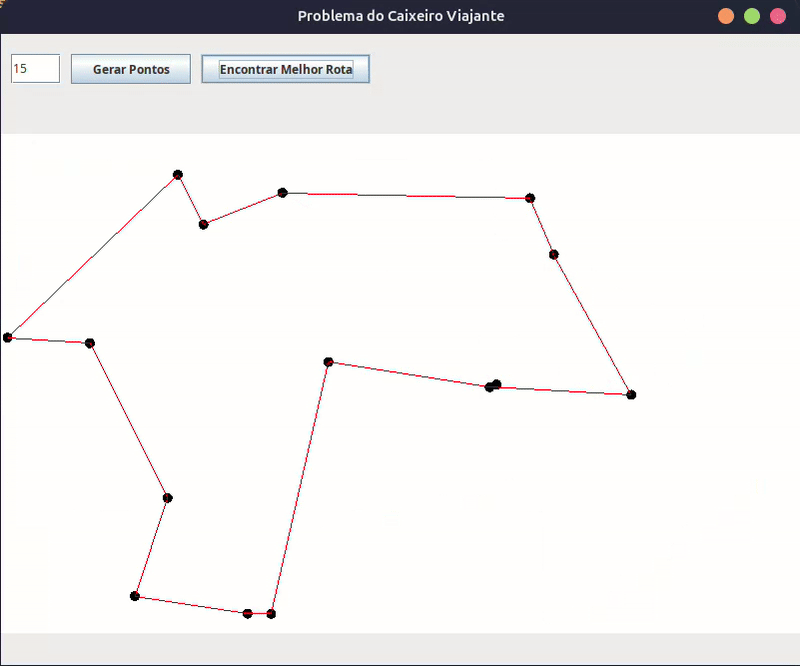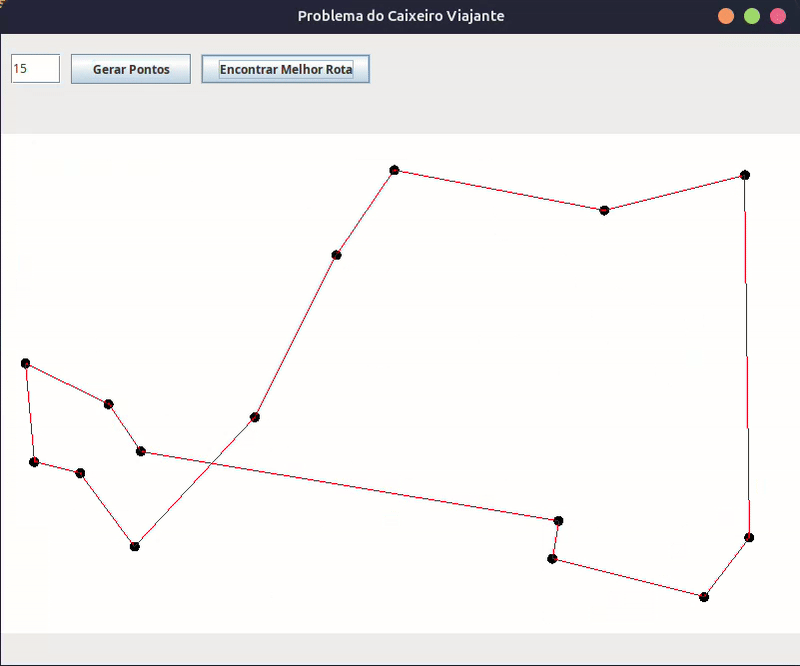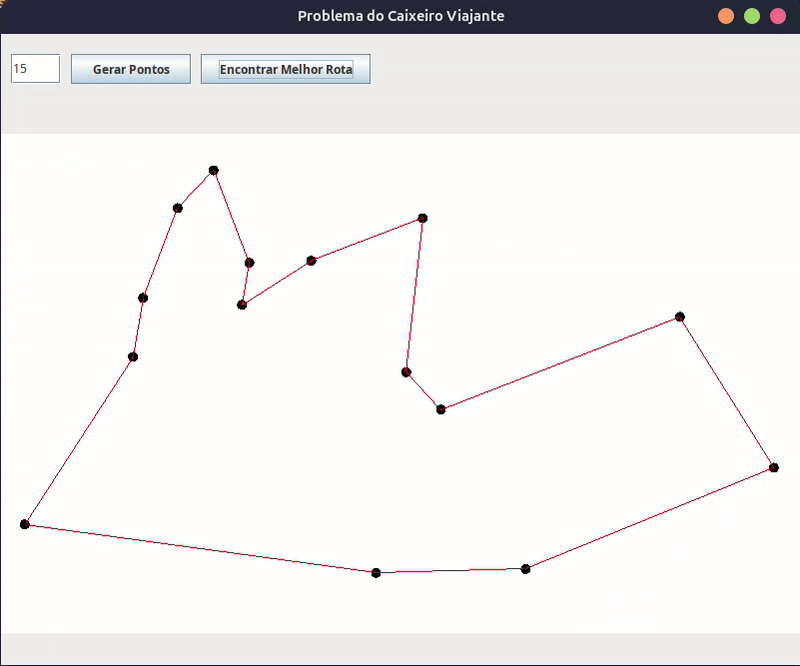
Como o programa funciona

  1. O usuário digita a quantidade de pontos e clica em “Gerar Pontos”.
  2. O programa cria pontos aleatórios na tela e os exibe.
  3. O usuário clica em “Encontrar Melhor Rota”.
  4. O algoritmo genético entra em ação, evoluindo rotas até encontrar uma solução otimizada.
  5. Assim que o melhor caminho for encontrado, uma animação exibe a rota sendo percorrida ponto a ponto.
Animação do algoritmo genético aplicado ao problema do caixeiro viajante

Considerações Finais

Este é um exemplo básico, mas ele ilustra bem como aplicar um algoritmo genético para resolver problemas de otimização complexos de forma visualmente intuitiva. Ademais, o código está bem estruturado, seguindo os padrões SOLID, o que facilita futuras expansões e manutenções.

Espero que tenha gostado deste post! Deixe seus comentários e sugestões, e vamos continuar explorando o mundo da programação juntos! 😉

Veja a seguir como desenvolver um jogo da velha usando o algoritmo minimax, para adeixar o adversário imbatível.

Deixe um comentário

Privacy Policy